분할 정복(Divide and Conquer)
- 여러 알고리즘의 기본이 되는 해결 방법, 엄청나게 크고 방대한 문제를 작은 단위로 쪼개어, 결과적으로 큰 문제를 해결하는 방법
- 퀵 정렬, 병합 정렬, 이분 탐색 등이 대표적 예시이다.
- Divide를 제대로 나누면 Conquer은 자동으로 쉬워지기 때문에 Divide를 잘 설계하는 것이 매우 중요하다.
- 분할 정복에서는 재귀 알고리즘이 많이 사용되는데, 이 부분에서 분할 정복의 효율을 깎아내릴 수 있다.
분할 정복의 설계
1. Divide(분할)
- 원래의 문제를 분할하여, 비슷한 유형의 하위 문제로 더 이상 분할이 불가능할 때 까지 나눈다.
2. Conquer(정복)
- 각 하위 문제를 재귀적으로 해결한다. 더 이상 나눌 수 없는 단위일 때의 탈출 조건(해결법)을 설정하고 해결한다.
3. Combine(조합)
- 정복한 문제들의 답을 통합하여, 원래 문제의 답을 얻는다.
뮤터블(mutable, 가변)
- 변경이 가능한 객체 ( 특정 주소를 계속 가리키고 있다 )
- 생성 후 자유롭게 값을 변경, 추가, 삭제 등이 가능하다
- 변수의 값을 변경하면 객체 그 자체를 업데이트 한다.
- call by reference(참조에 의한 호출)
이뮤터블(immutable, 불변)
- 변경이 불가능한 객체 ( 값에 따라 가리키는 주소 자체가 달라진다 )
- 생성 후 값 변경, 추가, 삭제 등이 불가능하다.
- 숫자, string, tuple 등
- 변수의 값을 변경하면 다른 객체를 “생성”하고 그 객체에 대한 참조로 업데이트 된다. ( 다른 주소를 가리킨다 )
- 만약 두 변수가 같은 값을 가지고 있다면, 두 변수는 같은 주소를 가리킨다. 변경하려는 값이 이미 메모리에 존재한다면, 생성하지 않고 그 주소를 가리킨다.
- call by value(값에 의한 호출)
그래프(Graph)
- 정점(vertex)들의 집합과 이들을 연결하는 간선(edge)로 이루어진 자료 구조
- 간선(edge)은 아크(arc)로 불리기도 하며, 정점(vertex)는 노드(node)라고도 불린다.
- 각 노드들은 트리와 다르게 계층 구조가 아니다.
그래프와 트리의 차이점
- 그래프는 트리를 포함한다.
- 트리는 비순환 방식, 그래프는 순환/비순환 선택 가능 ( 싸이클 허용 여부에 따라 갈린다 )
- 트리는 방향이 있음, 그래프는 방향 여부 선택 가능
- 트리는 계층 모델, 그래프는 네트워크 모델
싸이클(순환, Cycle)
- 자기 자신에서 출발해서 자기 자신으로 들어오는 간선
- 싸이클을 허용하면 순환 그래프, 아니라면 비순환 그래프이다.
모델(구조)
- 그래프의 구조를 나타낸다.
- 계층 모델(구조) : 트리처럼 상하 계층 구조가 있는 그래프
- 네트워크 모델(구조) : 네트워크처럼 이리저리 얽혀있는 경우
그래프의 종류 3가지
방향 그래프(Directed Graph)
- 노드 간 한쪽 방향으로밖에 접근할 수 없다면 방향 그래프이다.
무방향 그래프(Undirected Graph)
- 노드 간 양방향으로 접근할 수 있다면 무방향 그래프이다.
가중 그래프(Weighted Graph)
- 간선에 가중치(비용)가 적용된 그래프. ( 거리, 비용, 가중치 등 표현은 다양하다 )
- 방향/무방향 둘 다 적용될 수 있다.
트리 구조와 관련 용어

루트 : 가장 위에 위치하는 노드 (8번 노드)
리프 : 자식이 없는 노드(1, 4, 7, 13번 노드)
내부 노드(비단말 노드) : 리프를 제외한 노드(루트, 3, 6, 10, 14번 노드)
부모 : 어떤 노드와 연결된 “위쪽” 노드
자식 : 어떤 노드와 연결된 “아래쪽” 노드
형제 : 부모가 같은 노드
조상 : 어떤 노드에서 가지를 타고 위로 올라가면 만나는 모든 노드
자손 : 어떤 노드에서 가지를 타고 아래로 내려가면 만나는 모든 노드
레벨 : 루트에서 얼마나 멀리 떨어져 있는지를 나타내는 지표. 루트부터 0으로 시작해 가지를 타고 내려갈 때마다 1씩 증가. ex) 3번: 1레벨, 13번: 3레벨
차수 : 각 노드가 갖는 자식의 수. ex) 3번: 2, 14번: 1
- 모든 노드의 차수가 n 이하인 트리를 “n진 트리” 라고 한다.
- 모든 노드의 차수가 3 이하 : 삼진 트리
- 모든 노드의 차수가 2 이하 : 이진 트리
높이 : 루트에서 가장 멀리 있는 리프까지의 거리. -> 리프 레벨의 최댓값
서브트리 : 어떤 노드를 루트로 정의하고, 그 자손으로 구성된 트리를 서브트리 라고 한다.
ex) 3번이 루트라면 1과 6, 4, 7이 서브 트리
빈 트리(널(NULL)트리) : 노드와 가지가 전혀 없는 트리
순서 트리와 무순서 트리
- 순서 트리 : “형제 노드 간” 순서 관계가 있는 트리( 형제 간 정렬된 트리)
- 무순서 트리 : “형제 노드 간” 순서 관계가 없는 트리( 형제 간 정렬 안 된 트리)
기준을 순서 트리로 잡냐 무순서 트리로 잡냐에 따라 트리의 비교가 갈릴 수 있다.
순서 트리의 검색
BFS(너비 우선 탐색, Breadth-First-Search)
- 폭 우선 검색, 가로 검색, 수평 검색이라고도 함
- 낮은 레벨부터(루트부터) 왼쪽에서 오른쪽으로 검사한다.
- 가까운 노드부터 탐색하는 알고리즘
- 일반적으로 큐를 이용하고 파이썬에서는 deque를 사용하면 된다.
- O(N)의 시간복잡도를 가지며, 일반적인 경우 DFS보다 조금 빠르다
BFS 동작 방식
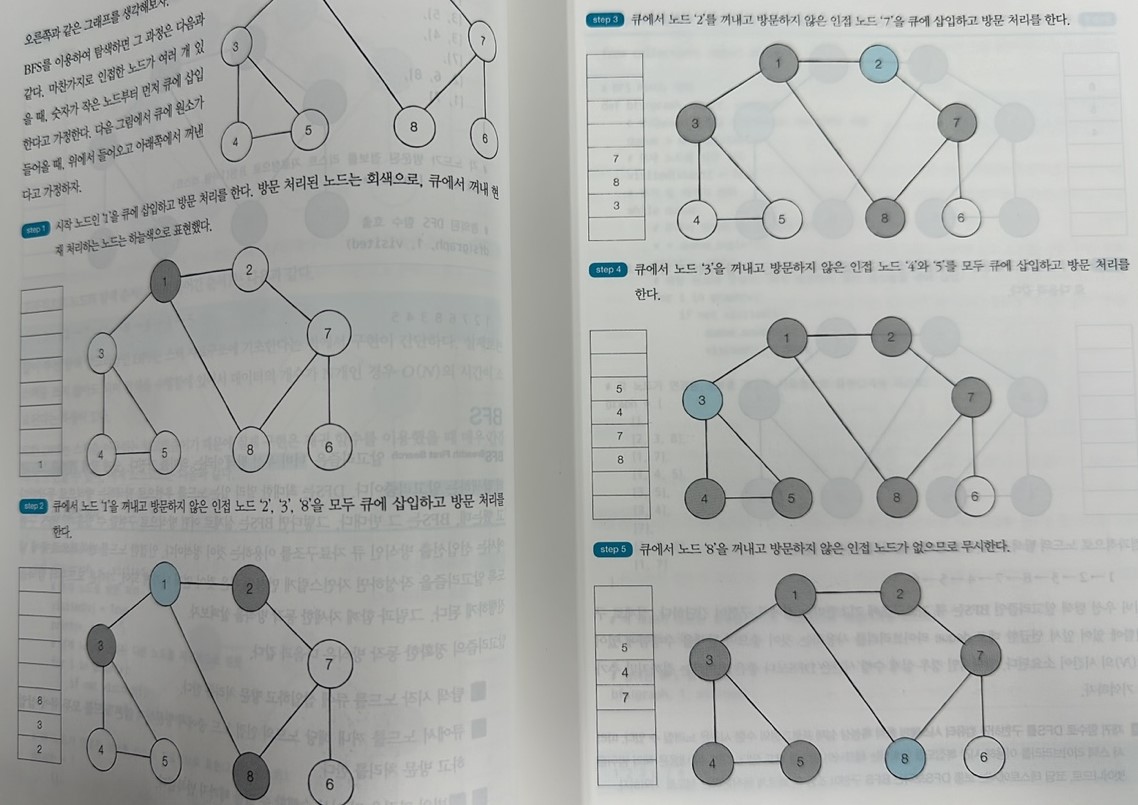
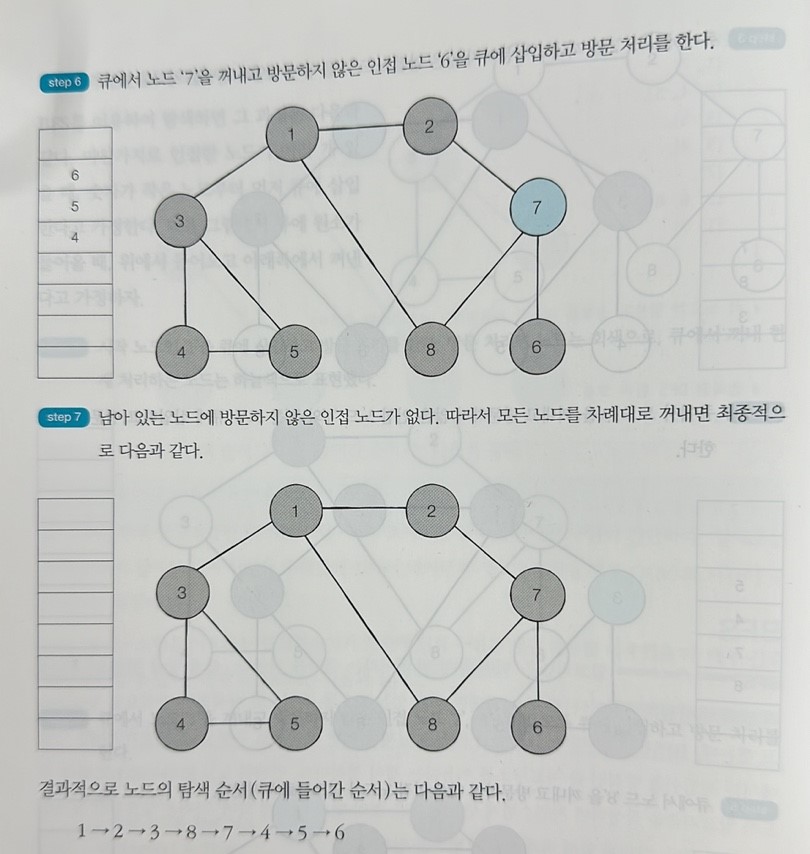
1. 탐색 시작 노드를 큐에 삽입하고 방문 처리
2. 큐에서 노드를 꺼내고, 해당 노드의 인접 노드 중 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리( 키가 낮은 노드를 먼저 삽입한다 )
3. 다시 선입선출 방식으로 노드를 하나씩 꺼내, 인접 노드를 큐에 넣고 방문처리 하는 걸 반복한다.
BFS 연습 코드 ( 파이썬 )
graph : 노드와 간선 연결 정보를 저장한다. 인덱스는 출발 노드 번호, 값은 연결된 노드이다. 인덱스 번호와 맞추기 위해 노드갯수 + 1 하였다.
ex) 1번 노드는 2, 3, 8번과 연결되어 있다
그리고 이 코드는 무방향(양방향) 그래프 기준이다.
visited : 방문 여부를 저장할 리스트. 인덱스 번호와 맞추기 위해 노드갯수 + 1 하였다.
먼저 deque에 시작 노드 번호를 추가하고, 시작 노드를 방문처리한다.
이후 모든 노드를 방문할 때까지 while 반복문을 돌며,
큐에 있는 노드를 꺼낸 후 방문을 알리는 출력을 하고,
해당 노드의 인접 노드 정보를 가져와 아직 방문하지 않았다면 deque에 추가하고 방문처리한다.
반복이 끝나면 이런 결과가 나온다.
12387456은 노드 방문 순서이다. 이 코드를 응용해서 다른 BFS 문제들도 풀 수 있다.
DFS(깊이 우선 탐색, Depth-First-Search)
- 세로 검색, 수직 검색이라고도 함
- 리프에 도달할 때까지 아래로 내려가는 것을 우선하는 검색 방법
- 리프에 도달했다면 다시 부모 노드로 돌아간 후 다른 자식을 찾아 리프까지 내려가는 걸 반복
- 멀리 있는 노드부터 탐색하는 알고리즘
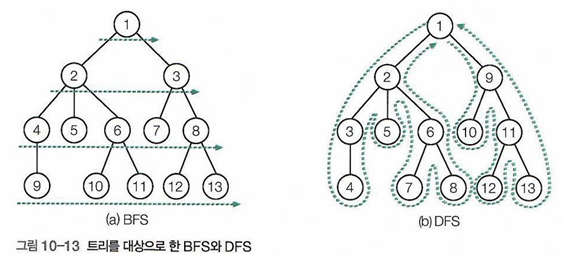
어느 시점에 실제로 노드를 방문하는지에 따라, DFS는 세 종류의 스캔으로 나뉜다.
전위 순회(preorder)
- 노드 방문 -> 왼쪽 자식 -> 오른쪽 자식
중위 순회(inorder)
- 왼쪽 자식 -> 노드 방문 -> 오른쪽 자식
후위 순회(postorder)
- 왼쪽 자식 -> 오른쪽 자식 -> 노드 방문
순회 순서가 헷갈릴 수 있는데, 트리를 서브트리 단위로 나누어 순회하면 덜 헷갈린다.
균형 검색 트리(이진 균형 검색 트리)
- AVL 트리(AVL tree)
- 레드 블랙 트리(red-black tree)
균형 검색 트리(이진이 아닌 트리)
- B 트리(B tree)
- 2-3 트리(2-3 tree)
이진 "검색" 트리의 특징 ( 그냥 이진 트리 아님 )
- 왼쪽 서브트리 노드의 키값은 자신(부모)의 노드 키값보다 작아야 함
- 오른쪽 서브트리 노드의 키값은 자신(부모)의 노드 키값보다 커야 함
- 따라서 키값이 같은 노드는 없다
- 구조가 단순함
- 중위 순회의 DFS를 통해, 노드값을 오름차순으로 얻을 수 있음
- 이진 검색과 비슷한 방식으로 아주 빠르게 검색할 수 있음
- 노드를 삽입하기 쉬움
서로소 집합(Disjoint Sets)
- 공통 원소가 없는 두 집합
- 서로소 집합 자료구조는 몇몇 그래프 알고리즘에서 매우 중요하게 사용된다. ex) 크루스칼 알고리즘( 최소 스패닝 트리를 구하는 알고리즘이다 )
서로소 집합 자료구조
- 서로소 부분 집합들로 나누어진 원소들의 데이터를 처리하기 위한 자료구조
- 서로소 집합 자료구조는, union과 find 2개의 연산으로 조작할 수 있음
- union : 2개의 원소가 포함된 집합을 하나의 집합으로 합치는 연산
- find : 특정 원소가 속한 집합이 어떤 집합인지 알려주는 연산
- 스택이 push/pop 으로 이루어졌던 것 처럼, 서로소 집합 자료구조는 union과 find 연산으로 구성된다.
- 서로소 집합 자료구조는 union-find 자료구조라고 불리기도 한다
- 서로소 관계인지 확인한다는 것은, 각 집합이 어떤 원소를 공통으로 가지고 있는지 확인하는 것과 같다.
'크래프톤 정글 > TIL' 카테고리의 다른 글
| [크래프톤 정글 5기] week02 알고리즘 주차 열두번째 날, 다익스트라 알고리즘(최단 경로 알고리즘), B-Tree (0) | 2024.04.01 |
|---|---|
| [크래프톤 정글 5기] week02 알고리즘 주차 열한번째 날, 파이썬 나눗셈, 위상 정렬 (0) | 2024.03.31 |
| [크래프톤 정글 5기] week01 알고리즘 주차 여섯번째 날, 해시 테이블, 힙, 우선순위 큐, 이진 트리, 피보나치 (1) | 2024.03.26 |
| [크래프톤 정글 5기] week01 알고리즘 주차 다섯번째 날, CPU, 인스트럭션, 퀵 정렬(Quick Sort) (0) | 2024.03.26 |
| [크래프톤 정글 5기] week01 알고리즘 주차 네번째 날, 스택, 큐, DFS, 그래프, 백트래킹, 이분 탐색 (2) | 2024.03.24 |