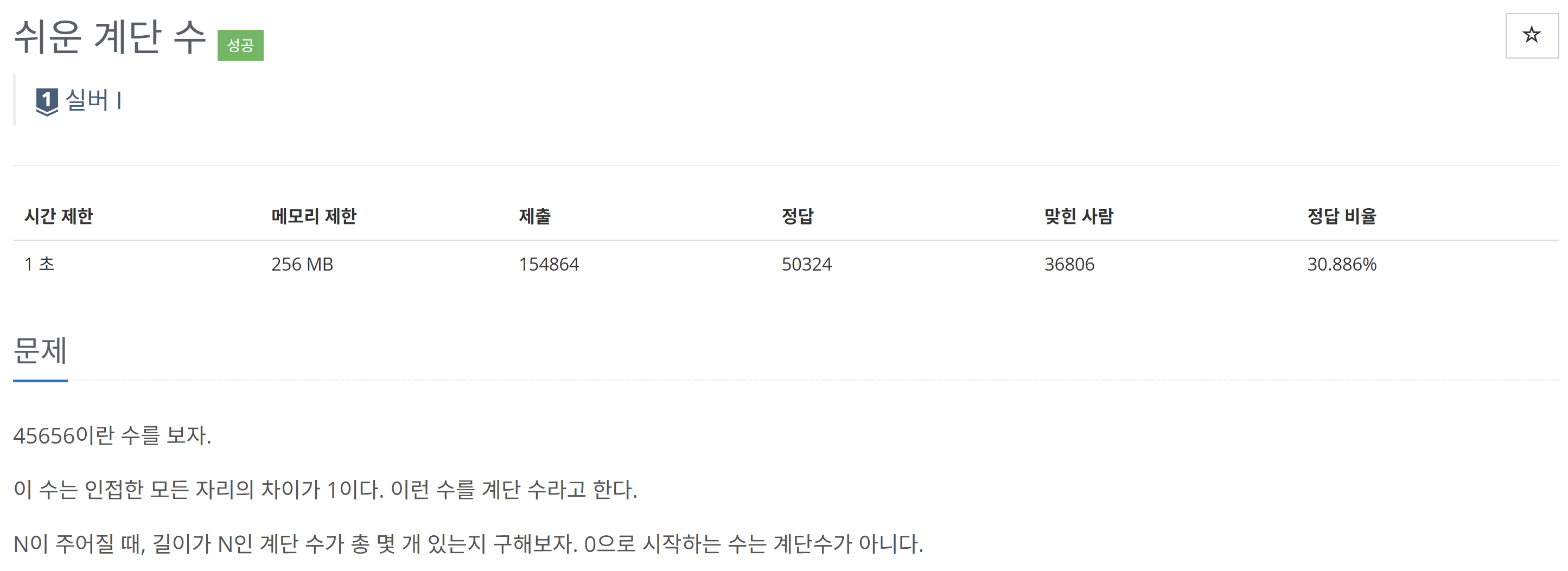
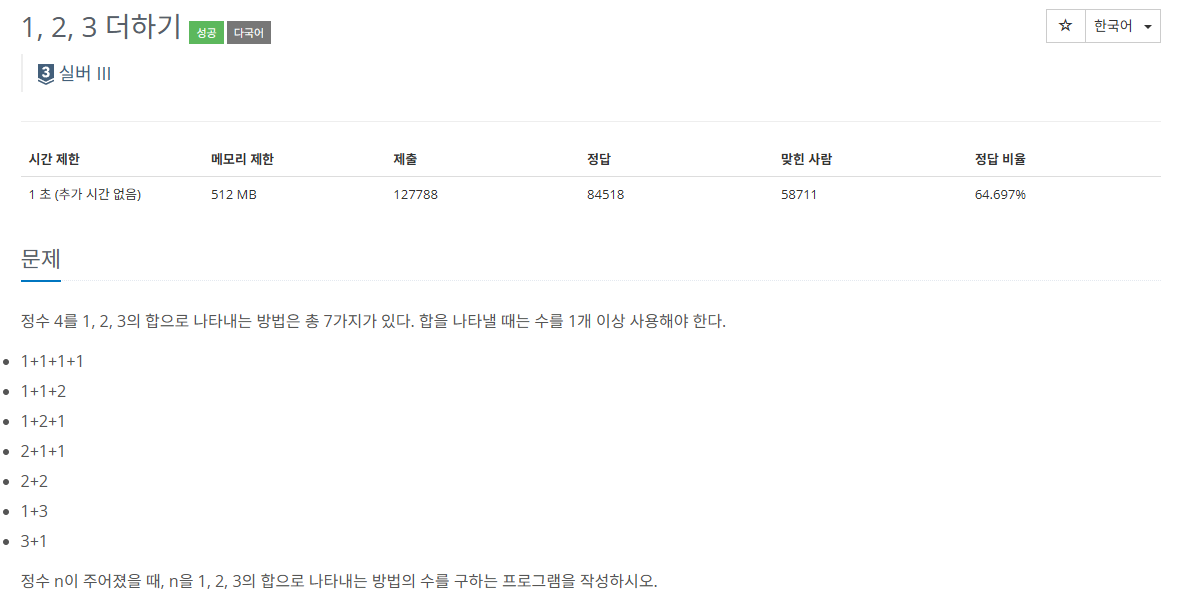
기본적인 피보나치 함수 문제이다. 일반적으로 재귀 또는 DP 형태로 풀 수 있다.이 문제에서는 시간제한이 0.25초로 짧기 때문에 DP로 풀어야 한다. import java.io.*;public class Main { static int zeroResult = 0; static int oneResult = 0; public static void main(String[] args) throws Exception { BufferedReader br = new BufferedReader(new InputStreamReader(System.in)); int T = Integer.parseInt(br.readLine()); for (int i = 0; i 첫 번째 시도 코드다. 최대 N이 40이라 ..