[프로그래머스 / python / Level 2] 도넛과 막대 그래프

문제

 

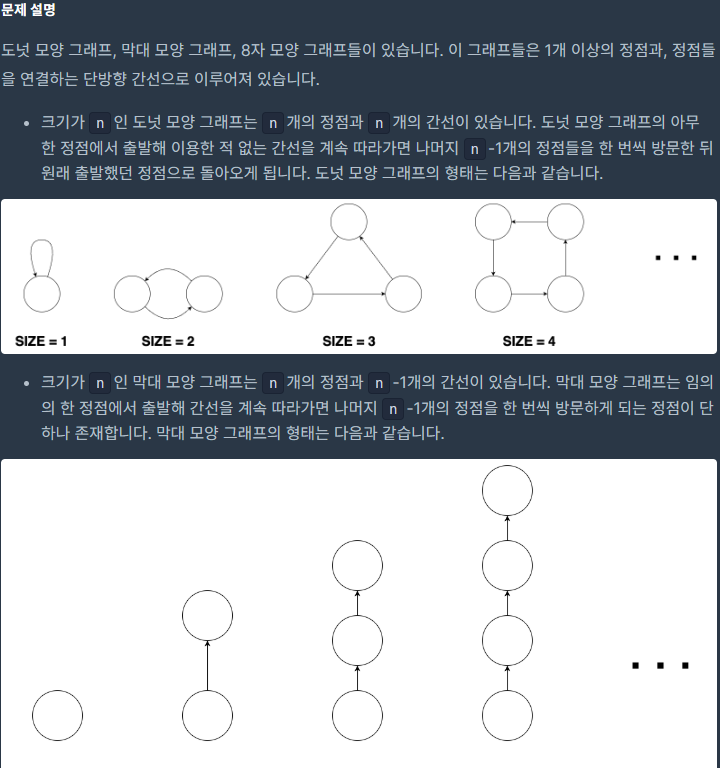
그래프 + 구현 문제이고, 2024 KAKAO WINTER INTERNSHIP 2번 문제이다.

분명히 Level 2인데, 레벨보다 훨씬 어렵게 느껴진다. 백준으로 치면 최소 골드 이상 정도는 되지 않나 싶다.

 

def solution(edges):
    
    """
    차수 0: 고립된 막대 그래프
    차수 1: 막대 그래프의 양 끝 정점
    차수 4: 8자 그래프의 중심점
    입차수가 0이고 출차수가 2 이상: 생성된 정점
    
    생성된 정점과 연결된 정점의 입차수를 1 빼줘야 한다.
    """
    
    """각 정점의 입/출차수 계산"""
    in_degree = dict()
    out_degree = dict()
    
    for a, b in edges:
        in_degree[b] = in_degree.get(b, 0) + 1
        out_degree[a] = out_degree.get(a, 0) + 1
        in_degree.setdefault(a, 0)
        out_degree.setdefault(b, 0)
    
    """생성된 정점 찾고 총 그래프 수 계산"""
    created_node = -1
    for node in in_degree:
        if in_degree[node] == 0 and out_degree[node] >= 2:
            created_node = node
            break
    total_graphs = out_degree[created_node]
    
    """생성된 정점과 연결된 정점의 입차수 1 깎기"""
    for a, b in edges:
        if a == created_node:
            in_degree[b] -= 1
    
    """차수0, 차수1, 차수4 정점 개수 계산"""
    solo_node = 0
    stick_ends = 0
    eight_centers = 0
    
    for node in in_degree:
        if node == created_node:
            continue
            
        total_degree = in_degree[node] + out_degree[node]
        
        if total_degree == 0:
            solo_node += 1
        elif total_degree == 1:
            stick_ends += 1
        elif total_degree == 4:
            eight_centers += 1
    
    """각 그래프 수 계산"""
    stick = solo_node + (stick_ends // 2)
    eight = eight_centers
    donut = total_graphs - (stick + eight)
    
    return [created_node, donut, stick, eight]

 

접근 방법부터가 까다롭다. 이 문제의 핵심은 "각 정점의 차수"를 파악하는 것이다.

 

각 정점은 차수에 따라서 특정된다.

입차수가 0이고 출차수가 2 이상: 생성된 정점

차수 0: 고립된 막대 그래프

차수 1: 막대 그래프의 양 끝 정점

차수 4: 8자 그래프의 중심점

 

또한, 생성된 정점과 연결된 정점의 입차수를 1 빼줘야 정확한 결과가 나온다.

도넛 그래프는 특정하기 어려운데, 총 그래프 수에서 막대/8자 그래프 수를 빼면 계산할 수 있다.

총 그래프 수는 "생성된 정점의 출차수" 이다.

 

차수로 접근하는 것에서 한번 어려웠고,

생성된 정점과 연결된 정점의 입차수를 빼주는 것에서 한번 걸렸고,

차수가 0인 고립된 막대 그래프를 고려하지 못해 또 한번 걸렸다.

 

Level 2답지 않게 복잡한 문제였다고 생각한다.

그러나 차수를 기준으로 그래프 문제에 접근할 수 있다는 새로운 시각을 얻을 수 있어 좋은 문제였다.